📓 Archive

  • Pricing
  • Chess
  • Syntax

    • 01-BINARY-TREE

    FGJ: Create:2024/02/22 Update: [2024-11-23]

    • Intro(BinaryTree) #

      • 二叉树 #

        • 定义 #

          二叉树的每个结点至多只有二棵子树(不存在度大于2的结点)，二叉树的子树有左右之分，次序不能颠倒。二叉树的第i层至多有2i-1个结点；深度为k的二叉树至多有2k-1个结点；对任何一棵二叉树T，如果其终端结点数为n0，度为2的结点数为n2，则n0=n2+1。

        • 性质 #

          1). 在非空二叉树中，第i层的结点总数不超过2i-1, i>=1;
          2) 深度为h的二叉树最多有2h-1个结点(h>=1)，最少有h个结点;
          3). 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1;
          4). 具有n个结点的完全二叉树的深度为log2(n+1);
          5). 有N个结点的完全二叉树各结点如果用顺序方式存储，则结点之间有如下关系：
              若I为结点编号则 如果I>1，则其父结点的编号为I/2；
              如果2I<=N，则其左儿子（即左子树的根结点）的编号为2I；若2I>N，则无左儿子；
              如果2I+1<=N，则其右儿子的结点编号为2I+1；若2I+1>N，则无右儿子。
          6). 给定N个节点，能构成h(N)种不同的二叉树，其中h(N)为卡特兰数的第N项，h(n)=C(2*n, n)/(n+1)。
          7). 设有i个枝点，I为所有枝点的道路长度总和，J为叶的道路长度总和J=I+2i。

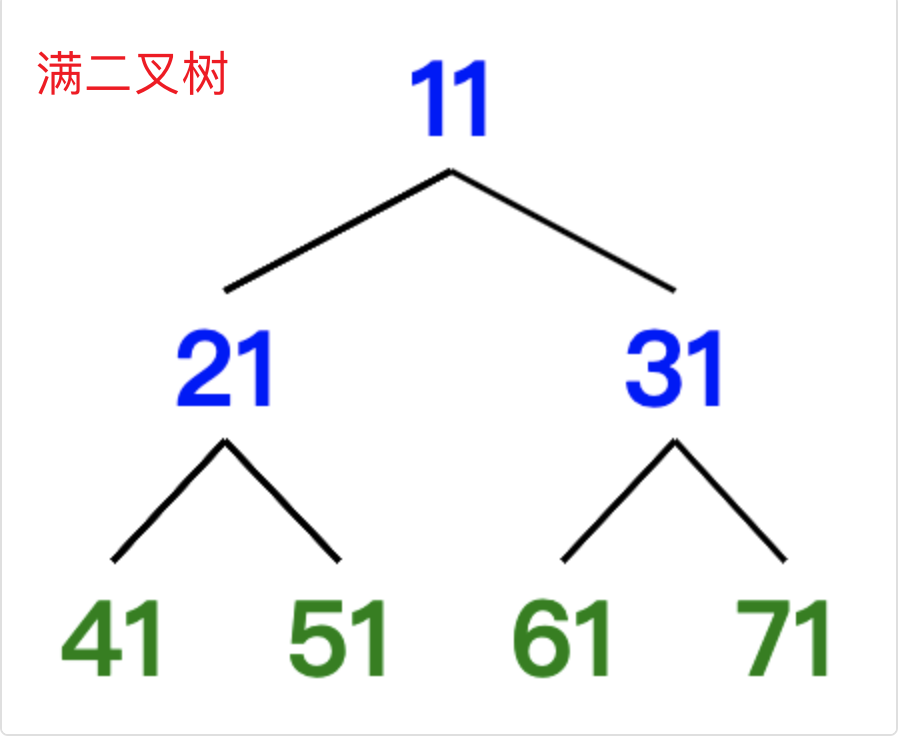
      • 满二叉树 #

        • 定义 #

          除最后一层无任何子节点外，每一层上的所有结点都有两个子结点。也可以这样理解，除叶子结点外的所有结点均有两个子结点。节点数达到最大值，所有叶子结点必须在同一层上。

        • 性质 #

          1) 一颗树深度为h，最大层数为k，深度与最大层数相同，k=h;
          2). 叶子数为2h;
          3). 第k层的结点数是：2k-1;
          4). 总结点数是：2k-1，且总节点数一定是奇数。

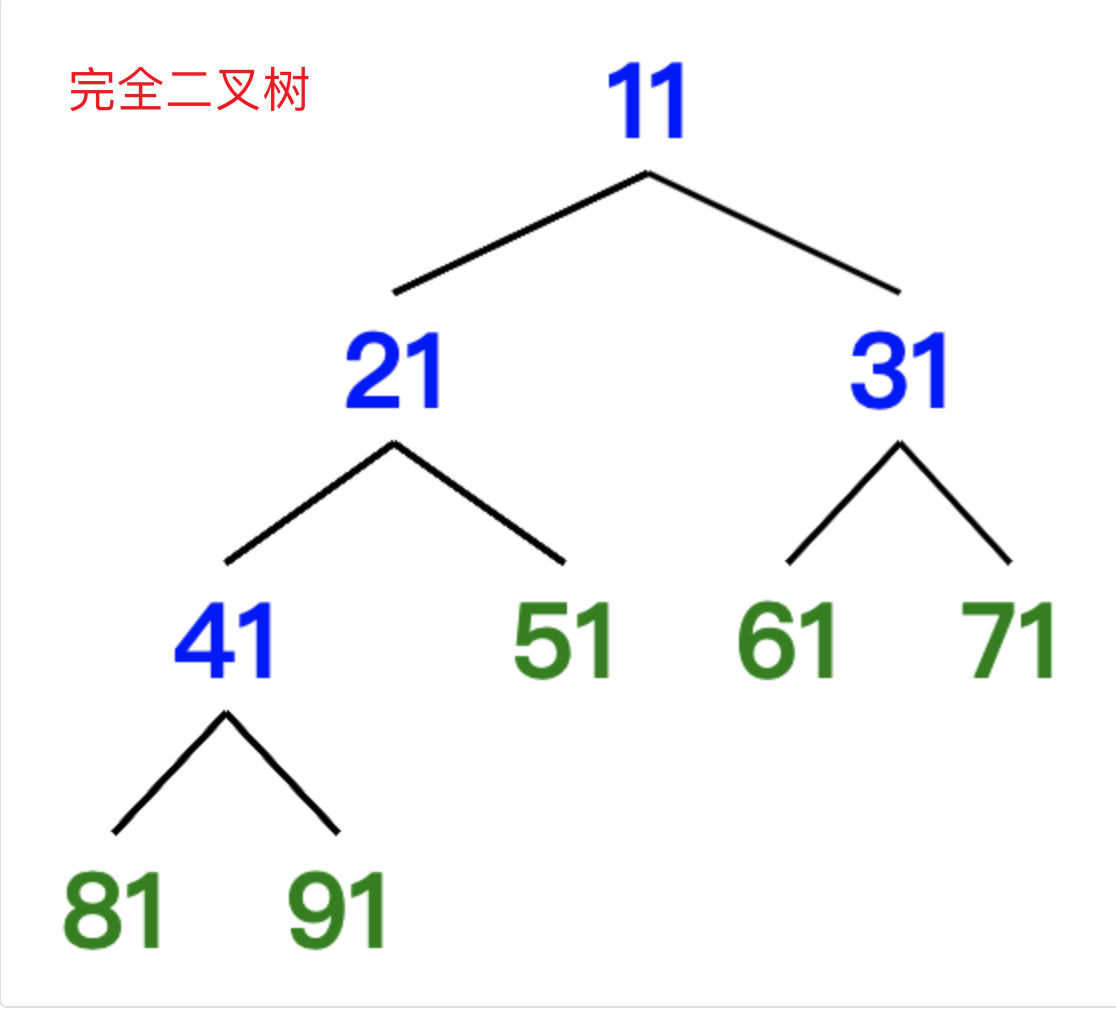
      • 完全二叉树 #

        • 定义 #

          若设二叉树的深度为h，除第 h 层外，其它各层 (1～(h-1)层) 的结点数都达到最大个数，第h层所有的结点都连续集中在最左边，这就是完全二叉树。

          完全二叉树是效率很高的数据结构，堆是一种完全二叉树或者近似完全二叉树，所以效率极高，像十分常用的排序算法、Dijkstra算法、Prim算法等都要用堆才能优化，二叉排序树的效率也要借助平衡性来提高，而平衡性基于完全二叉树。

      • 示例 #

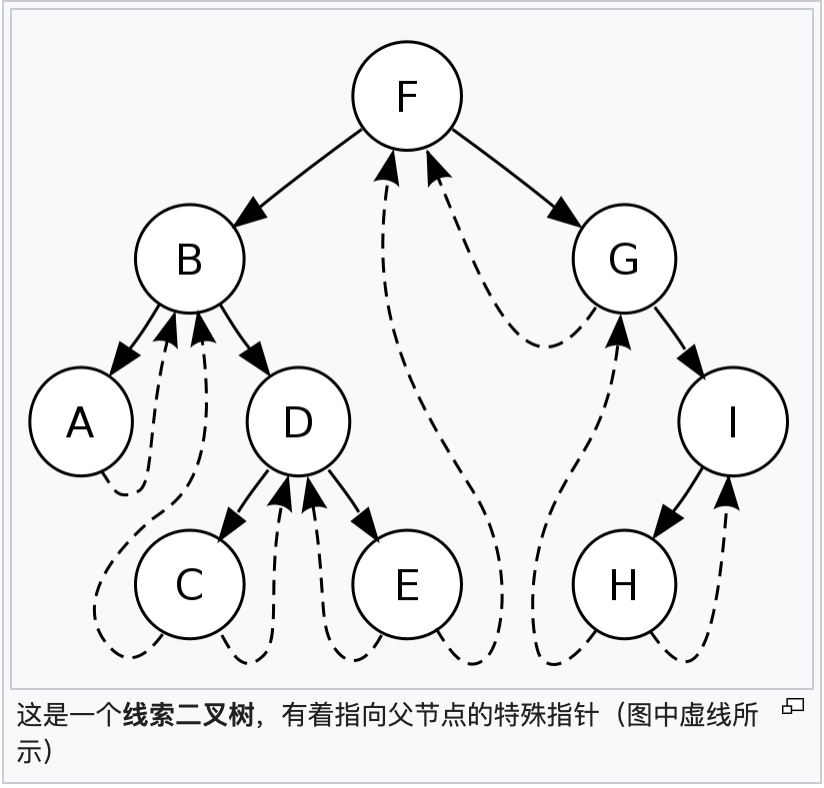
      • 线索化二叉树 #

        wiki: 在计算机科学中，线索二叉树（或称引线二叉树）是添加了直接指向节点的前驱和后继的指针的二叉树。

        图解与代码 #

        public void threadedTree(Node node){
    if(node == null){ return;}
    // 中序遍历
    threadTree(node.getLeft());

    if(node.getLeft() == null){
        node.setLeft(pre);
        node.setLeftType(1);
    }

    if(pre != null && pre.getRight() == null){
        pre.setRight(node);
        pre.setRightType(1);
    }

    // 保存当前节点，为下一次遍历做准备。
    pre = node;

    threadTree(node.getRight());
}

    • Implement #

      • Node #

        class Node {
    public int value;
    public Node left,right;

    public Node(int value) { this.value = value;}

    public Node(int value, Node left, Node right) {
        this.value = value;
        this.left = left;
        this.right = right;
    }
}

      • 遍历 #

        // 前序遍历
public static void recursionPreOrderTraversal(Node tree){
    if(tree!= null){
        System.out.print(tree.value + ",");
        recursionPreOrderTraversal(tree.left);
        recursionPreOrderTraversal(tree.right);
    }
}
// 中序遍历
public static void recursionInOrderTraversal(Node tree){
    if(tree!= null){
        recursionInOrderTraversal(tree.left);
        System.out.print(tree.value + ",");
        recursionInOrderTraversal(tree.right);
    }
}
// 后序遍历
public static void recursionPostOrderTraversal(Node tree){
    if(tree!= null){
        recursionPostOrderTraversal(tree.left);
        recursionPostOrderTraversal(tree.right);
        System.out.print(tree.value + ",");
    }
}

      • 后序和中序构建 #

        public class BuildBinaryTree {

    private  Map<Integer,Integer> inMap = new HashMap<>();
    private int index_root = 0;
    private int [] postOrder = null;

    public void init(int[] inOrder,int[] postOrder){
        for (int i = 0; i < inOrder.length; i++) {
            inMap.put(inOrder[i],i);
        }
        this.postOrder = postOrder;
        index_root = postOrder.length - 1;
    }

    public Node build(int index_left,int index_right){
        if(index_left > index_right) return null;

        int root_value = postOrder[index_root--];
        Node root = new Node(root_value);
        int _left = inMap.get(root_value);
        root.right = build(_left + 1,index_right);

        root.left = build(index_left,_left - 1);
        return root;
    }

    @Test
    public void test(){
        int[] postOrder = {9,15,7,20,3};
        int[] inOrder = {9,3,15,20,7};

        init(inOrder,postOrder);
        Node root = build(0,inOrder.length - 1);
    }
}

    Reference #

    comments powered by Disqus