COMPLEMENT
Intro(Complement) #
重新认识计算机中的数字表示 #
主要以一个字节,8比特位进行分析
首先要知道计算机中的数字表示有空间限制,比如 java 中 byte 类型就用一个字节(8 bit)表示,而 int 得用 4byte(32 bit)。而且 java 默认都是有符号的,也即第一个比特位表示符号,一个byte 类型的变量可表示的值就是 \(00000000\) - \(11111111\)。
还有一点至关重要,就是进位后的值超出 8 位后会截断。比如 \(11111111 + 1 = 1{\hspace{0.5em}}00000000 ==截断==> 00000000 \),要不然就没法循环了,跟钟表一样,到极限得归位。
至于这些值表示的实际意义,可以在下面慢慢进行分析。(先不用考虑补码)1).: 首先分析正数,总共 8 位,一个符号位占一个[0],剩下的 7 位表示值的话就就是 \(00000000\) - \(01111111\) 表示数值 0 到 127,这个毋庸置疑的。2).: 不管一个负数怎么表示,都应该符合我们的理性认知。比如 -1 + 1 的值肯定是 0 的。3).: 现在有了正数值比如 1 (\(00000001\)),加一操作后肯定等于 0。也即 \(00000001\) + \(8(*) = 00000000\)4).: 目前只有让 \(8(*)\) 这个未知值在加完后整体位溢出,被截断,才能达到加完一个值后更小。5).: 所以此处的 \(8(*)\) 二进制表示应该是 \(11111111\),加完 \(00000001\) 后得到 \(1{\hspace{0.5em}}00000000\),截断,然后正好等于 \(00000000\)。6).: 所以才让这个二进制 \(11111111\) 表示的 -1。7).: 其他情况依次了类推,重要的是理解截断才能循环。再举个例子(-128)。8).: 已知上述得出的 -1\((11111111)\),和127\((01111111)\),所以 -128 \(8(*)\) + 127 \(01111111\) = -1 \(11111111\)9).: 后面的值在二进制表示上要比被加数大,所以这次不用截断,给 \(8(*)\) 值设为 \(10000000\) 即可。也就是 -128 = \(10000000\)
为了更好的理解数据的分布,可以画一个圆来表示,方便记忆。范围: \([{\color{red}-(2^{8*size-1})}\) , \({\color{red}(2^{8*size-1})-1}]\),size = 1 时:[-128, 127].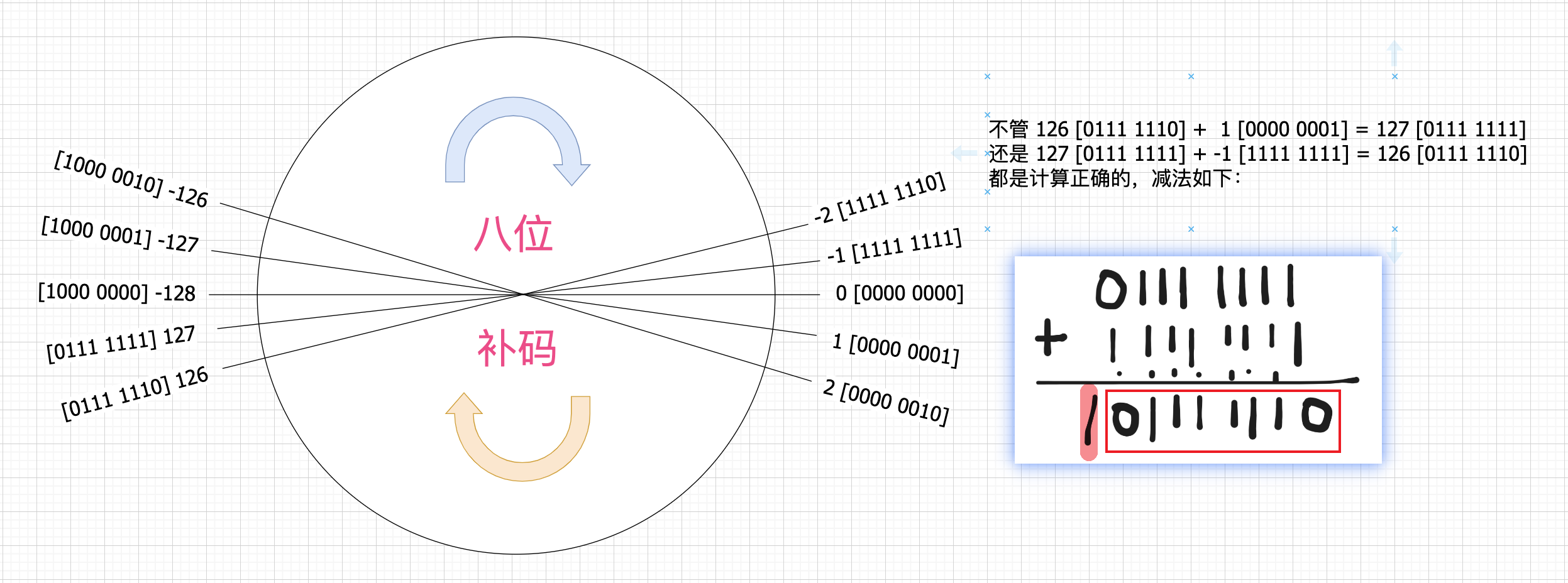
认识补码 #
原码,反码定义:
原码: 最高位为符号位,剩余存放 真值 绝对值。反码: 正数的反码等于原码,负数的反码是除符号位之外全部取反。
其实上述得出的二进制表示在计算机中被成为补码,不管是正数的也好,还是负数的也好。只是正数的补码与原码相同,而负数的补码与原码的关系可以推算出来,比如:
\([-1_补 = 1111111]\) 减一后 ==> \([11111110]\) 所有位置取反 ==> \([1_{补|原} = 00000001]\)
\([-2_补 = 1111110]\) 减一后 ==> \([11111101]\) 所有位置取反 ==> \([2_{补|原} = 00000010]\)
\([-128_补 = 10000000]\) 在 8 bit 中只有补码的形式。
\([-105_补 = 10010111]\) 减一后 ==> \([-105_反 = 10010110]\) 除符号位取反 ==> \([-105_{原} = 11101001]\)
\([-105_补 = 10010111]\) 减一后 ==> \([-105_反 = 10010110]\) 所有位置取反 ==> \([105_{原|反|补} = 01101001]\)
也就是对于一个负数来说,补码等于(其反码 + 1)。(或者:等于它的正数值对应任意(原,反,补)码的 所有位 按位取反加一)在线计算小工具 105 -105 127 -127 原码 01101001 11101001 01111111 11111111 反码 01101001 10010110 01111111 10000000 补码 01101001 10010111 01111111 10000001 辅助验证 #

认识移码 #
移码(Bias或Offset Binary)是一种在计算机系统中用于表示有符号数的方法,特别是在 浮点数 标准如 IEEE 754 中广泛使用。它的主要作用是为了简化数值比较和排序操作,使得所有数值——包括正数和负数——可以被视为无符号整数进行处理,从而利用硬件对无符号数的高效比较机制。
对于 8 位的移码来说,相当于其补码 + 偏移量(范围个数的一半: 256 / 2 = 128 = \(2^{8-1}\)),比如:1.\(-105_移 = ([-105_补 = 10010111] + 128) = 00010111\)2.\(-127_移 = ([-127_补 = 10000001] + 128) = 00000001\)
通过以上观察:也可以理解移码为 其补码的符号位取反。Caution
之所以方便比较和排序是因为:可以不用考虑符号位,直接全部按位比较了。比如:
\( {\color{red}(2, [2_移 = 1000 0010])} > {\color{#FF4500}(1,[1_移 = 1000 0001])} > {\color{#FF6347}(-2,[-2_移 = 0111 1110])} > {\color{#FF7F50}(-127,[-127_移 = 0000 0001])}\)
Reference #